一、如何定义最大公因数
如果c是a的因数,c也是b的因数,那么我们称c是a和b的公因数。一般来说,两个数的公因数不止一个,我们把其中最大的一个公因数称为这两个数的最大公因数。多个数之间的公因数和最大公因数也可以用类似的方法定义。
互质:如果两个数的最大公因数为1,则称这两个数互质。
三、求最大公因数的方法
1、分解质因数法
求最大公因数与最小公倍数主要有质因数法、短除法两种方法,接下来我们先来学习分解质因数法。
考生可采用分解质因数的方法求两个整数的最大公因数与最小公倍数。下面以两个数为例进行讲解,多个整数的情况可以类推。
分解质因数:每个合数都可以写成几个质数相乘的形式,其中每个质数都是这个合数的因数。
举例说明:求24和60的最大公因数与最小公倍数?

最大公因数是两个数所有公有质因数的乘积。24、60的公有质因数是2、2、3,所以24和60的最大公因数是2×2×3=12。
2、短除法。
短除符号就是除号倒过来,在除法中写除数的地方写两个数共有的质因数,然后写下两个数被公有质因数整除的商,之后再除,以此类推,直到结果互质为止。如:
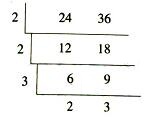
所以24、36的最大公因数为2×2×3=12(左侧3个数之积)。
最小公倍数为2×2×3×2×3=72(左侧3个数与下边2个数之积)。
三个数的情况与两个数的情况有所区别,要仔细体会。以下举例说明,如求12、30、150的最大公因数与最小公倍数。
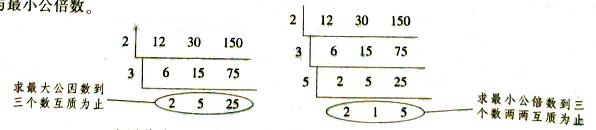
12、30、150的最大公因数为2×3=6,最小公倍数为2×3×5×2×1×5=300。
通过以上的学习,我们来看一道练习题,帮助大家加强巩固练习。
有三根铁丝,一根长54米,一根长72米,一根长36米。要把它们截成同样长的小段,不许剩余,每段最长是多少米?
A.8
B.12
C.18
D.24
正确答案:C
解析:要截成同样长的小段,则截的长度应为54、72、36的公因数。题干要求最长的长度,则应为三个数的最大公因数,利用短除法可求得54、72、36的最大公因数是18。
点评:此题也可用代入排除法。题中要求的是每段最长的长度,那么应该从最大的D项开始代入,这时会发现24不是54的因数,排除,再代入C项,正好满足条件。







